Futoshiki
Calcudoku
![]()
Consecutive Sudoku
Oddpair Sudoku
Pro
Sudoku
![]()
Looking for puzzles for your book, magazine or newspaper?
|
How to solve Kropki Sudoku
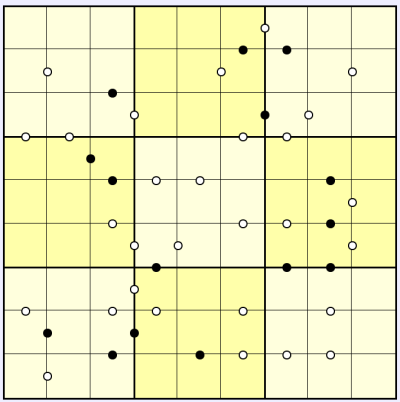
Kropki Sudoku puzzles add black (o) and white (o) circles to a regular Sudoku puzzle. All pairs of touching squares which contain consecutive values (such as 2 & 3 or 6 & 7) are marked with a white circle: o. Also, all pairs of touching squares which contain values where one number is exactly twice the value of the other (such as 2 & 4, or 4 & 8) are marked with a black circle: o. This applies to left/right, up/down touching only - there are no diagonal markers. All possible o and o are given, so if there is no circle between two touching squares then they are not consecutive and one is not double the value of the other. When 1 & 2 touch, then either a white circle or a black circle will be given, since 1 & 2 are both consecutive and also one is double the value of the other. Standard Sudoku rules also apply: place 1 to 9 (or 1 to whatever the width of the puzzle is) once each into every row, column and bold-lined box. So to summarise, o indicates that the touching values are one of 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8, or 8&9. And o indicates that the touching values are one of 1&2, 2&4, 3&6 or 4&8. If there is no marker then none of these pairs is possible.
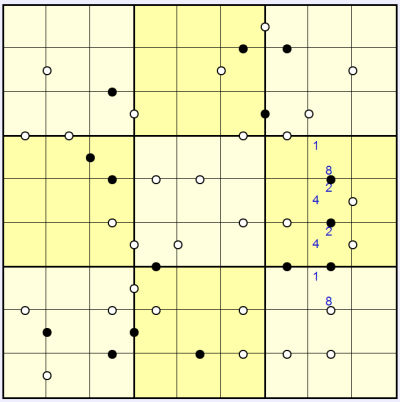
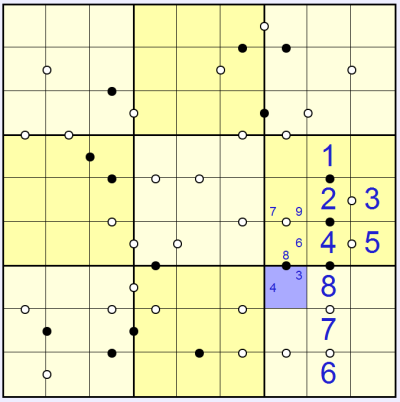
In this example puzzle there are various places you could start solving, but I've chosen to consider the column of black circles in the right-centre 3x3. Since these are all in the same column the sequence must be 1-2-4-8 or 8-4-2-1. I've made note of this using candidate pencilmarks:
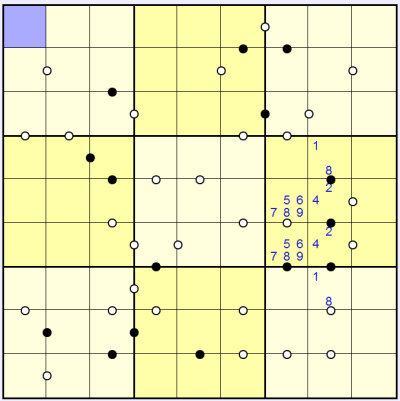
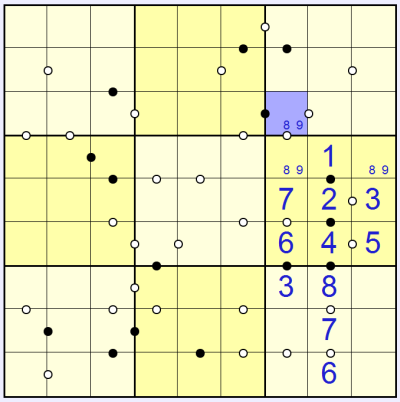
Now the left-most white consecutive squares in the centre-right 3x3 can't contain 1 or 3 because the 2 and 4 are already used in this 3x3 box, so we can mark these squares with pencilmark options as follows:
But in order for the black 'double pair' circle below this consecutive pair to be valid we can in fact prune the list of possibilities to this:
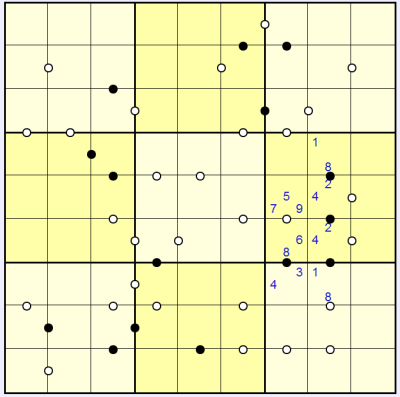
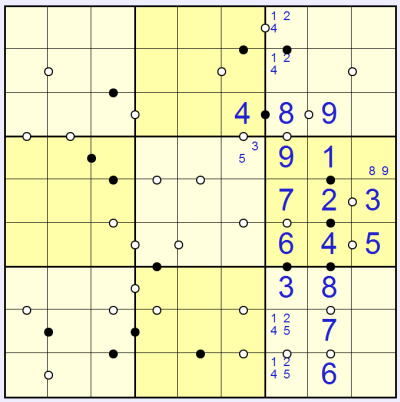
We can place our first full digit by considering column 8, below the 1-2-4-8/8-4-2-1 we have already marked in. The white dot next to the lower 1/8 square must link to 7 or 9, because the 2 is already accounted for in this column. The 7 or 9 in turn must link to 6, because the 8 is already used. So we have:
We can then follow the chain of circles back up to get:
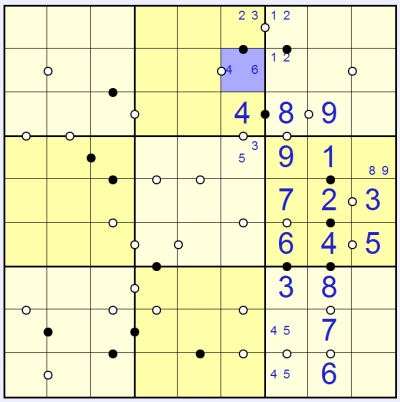
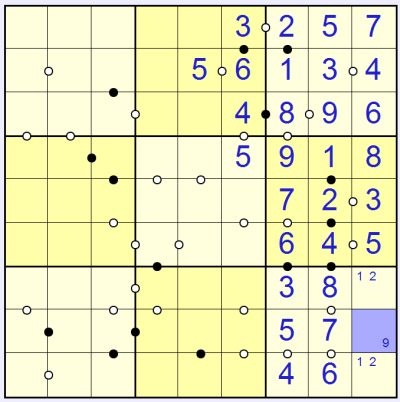
Now consider the square marked in blue above. It is next to the 8 but there is no circle between them. Therefore it cannot be the 4 option because double this is 8, and there would need to be a black circle marked. So the solution here must be:
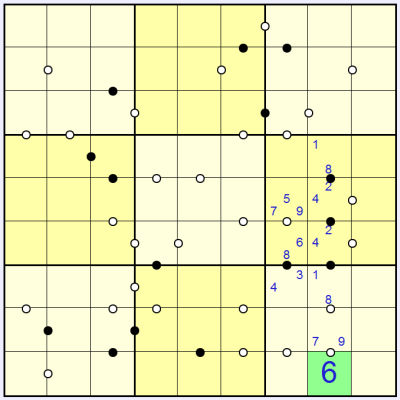
And now we can see that the square marked in blue in this picture (above) cannot be 9 because there could be no solution to the square to its left (or similarly you can say it can't be 9 because there could be no solution to the square to its right either).
Marking in options for the other squares in the seventh column (above), we can see that the 5 can only go in one of the bottom two squares, which gives:
And from here the square highlighted in blue must of course be 6, and similarly in the bottom-right 3x3 the 5 cannot touch the 6 since there is no circle between them. If we resolve these squares and place other forced numbers we end up with:
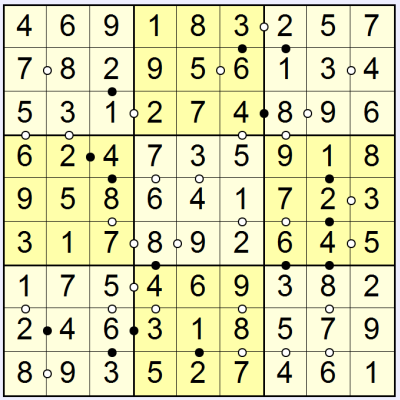
Note how in the bottom-right 3x3 the options 1, 2 and 9 are left for the right-most three squares. Because these all touch, and there are no circles between any of them, the 9 has to go in the middle. If it didn't then the 1 or the 2 would be touching the other of the pair, breaking the rules. We can now continue to solve to reach the final result:
|