Sudoku XV puzzles (which are nothing to do with Sudoku-X) add two extra symbols to a regular Sudoku puzzle. All pairs of touching squares which add up to a total of 5 or 10 are marked with a 'v' or 'x' respectively. This applies to left/right, up/down touching only - there are no diagonal markers.

All possible 'v's and 'x's are shown in the puzzle, so if there is no 'v' or 'x' between two touching squares then they do not add up to 5 or 10.

This means that every time a 1 & 4 touch or a 2 & 3 touch there is a 'v' between them. And every time a 1 & 9, or 2 & 8, or 3 & 7, or 4 & 6 touch there is a 'x' between them.

Standard Sudoku rules also apply: place 1 to 9 (or 1 to whatever the width of the puzzle is) once each into every row, column and bold-lined box.

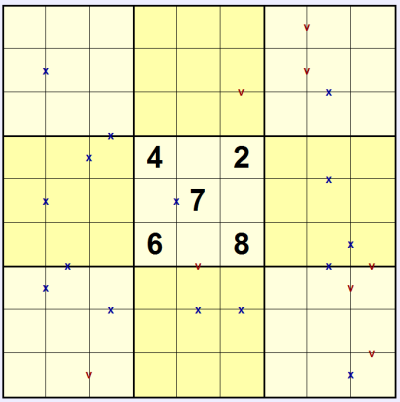
In the example puzzle shown here you can immediately place a 3 in the centre 3x3 thanks to the 'x' touching the 7:

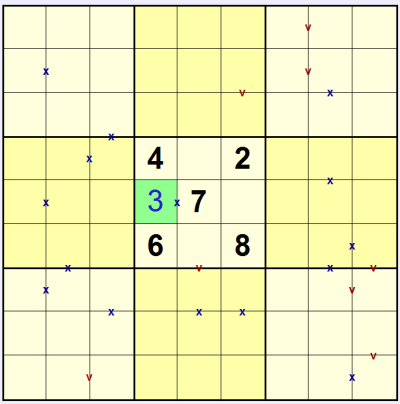
The square with the 'v' at the bottom of the centre 3x3 can only contain a 1, since 2, 3 and 4 are already used in this 3x3, so we can solve this and the squares below linked by the 'v' and the 'x':

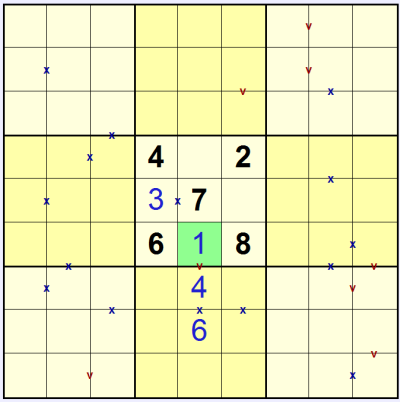
We can now start to use small 'pencilmark' digits to keep track of potential valid values in each square. We can see that the 'v' in the top-centre 3x3 must be made up of 1 & 4 in some order (since there is already a 2 in that column). If we mark this in we can then see that the only option for the 'x' in the same column is 3 & 7:

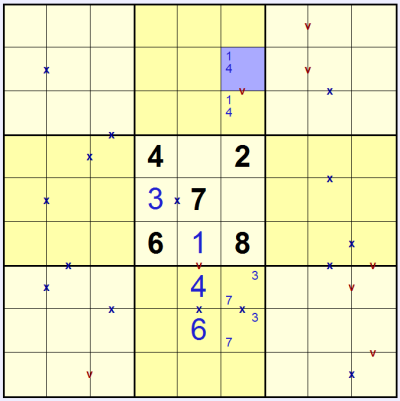
With the 1 & 4 in the top-middle 3x3 we know that the 'v' to the right of the 1 & 4 in the top-right 3x3 must be solved with 2 & 3, and so the other 'v' in that box must be 1 & 4. Similarly looking in the middle-right 3x3 box we can see that the 'x' must be solved with 3 & 7, which since one square also shares a 'v' the solution can only fit in one way:

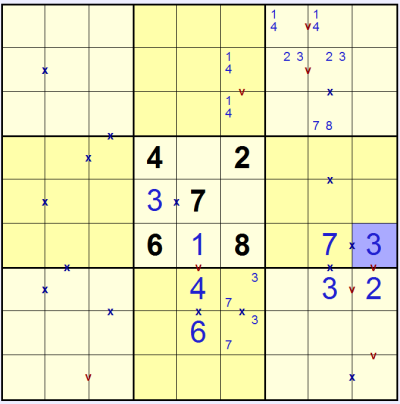
We can use these placements to work out the actual values in some previously pencil-marked squares.

We can also place a 2 in the middle-right 3x3, highlighted in green in the picture below. To work out how, note that the 2 in this 3x3 cannot be in the upper row or the right-most two columns. It also can't be in the bottom-left square of the 3x3 because it would touch the 8 in the middle 3x3 - and without an 'x' marked this would be an illegal move since the squares would sum to 10. So:

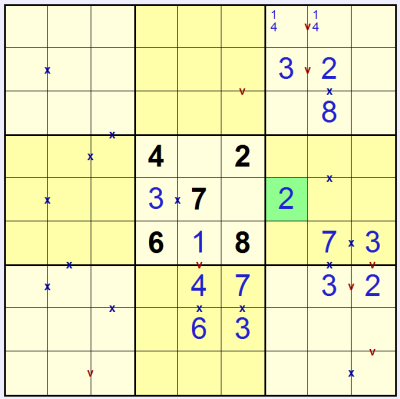
You can now continue to solve the puzzle to reach the final result:

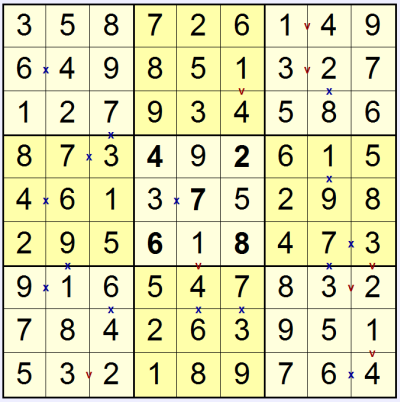
One final comment: it's also sometimes helpful to note that, because the number 5 cannot be part of either a 'v' or 'x' pair, that if there is only one square in a region without a 'v' or 'x' touching it then that square must contain a 5.